Meaning of pH

pH of the water.

PH is a measure of the concentration of hydrogen ions (H⁺) in an aqueous solution. The term comes from the Latin pondus hydrogenii (“Amount of hydrogen”). We will not only focus on the pH of the water, but we will talk about the pH in general.

Later it is shown that the concentration of hydrogen ions has a direct relationship with the concentration of hydroxide ions (OH^–), so the pH is also a measure of the concentration of the latter.

When an electrolyte dissolves in water, it generates a cation and an anion.

Water also dissociates and does so to a lesser or greater degree, depending on the electrolytes dissolved in it.

The equilibrium reaction representing the dissociation of water was originally believed to be:

H₂O ???? H⁺ + OH^– 

H⁺ is the hydrogen ion, and OH^– is the hydroxide ion. Today we know that the reaction is:

2 h₂O ???? H₃O⁺  + OH^– 

H₃O⁺ is the hydronium ion, and OH^– is the hydroxide ion. For practical purposes, even today, when we refer to the hydrogen ion, it is actually the hydronium ion. In accordance with this custom, from this point on, we will call what the hydronium ion really is the hydrogen ion.

Most dissociation reactions reach chemical equilibrium. When this is reached, the product of the concentration of the ions formed (in terms of molar concentration) is called the “reaction equilibrium constant”. In the case of water:

K_w = [H⁺] [OH^– ]

K_w is the equilibrium constant of the reaction. For totally pure water and at 25 ° C, the molar concentration of hydrogen ions (in gmol / L) is:

[H⁺] = 1 x 10^-7

And the molar concentration of hydroxide ions is:

[OH^– ] = 1 x 10^-7

Therefore:

K_w = [H⁺] [OH^–] = 1 x 10^-14           (1)

This relationship is true even if the water in question contains hydrogen ions or hydroxide ions from dissolved electrolytes that have been added to it.

 

Therefore, if the concentration of the hydrogen ion decreases, the concentration of the hydroxide ion increases by such a proportion that the product of both concentrations remains 1×10^-14 at 25 ° C.

Since the numerical values of the concentrations of hydrogen ions or hydroxide ions in a solution are usually very small numbers, the chemist Søren Sørensen proposed pH as a unit of measurement for the concentration of hydrogen ions in aqueous solutions:

pH = – log [H⁺]

Water behaves in such a way that the range of values that the pH can have is from 0 to 14.

To measure the concentration of the hydroxide ion, pOH can be defined as:

pOH = -log [OH^– ]

It is valid to obtain the negative value of the logarithm of each addend that makes up the equation (1):

-log K_w = -log [H⁺] – log [OH^–] = -log (1 x 10^-14)

-log K_w  = -log [H⁺] – log [OH^–]  =  14

From the definition of pH and pOH, it can be inferred that:

pK_w  = pH + pOH = 14

There are equipment capable of measuring pH, called potentiometers. Considering the definition of pH, by increasing the concentration of hydrogen ions in the water, the pH decreases and by increasing the concentration of hydroxide ions, the pH increases.

It can also be seen that, if the pH decreased by one unit, the hydrogen ion concentration increased 10 times. In water with pH 5, the hydrogen ion concentration is 100 times higher than in water with pH 7.

The same applies to the opposite side: in a water with a pH of 13, the concentration of hydroxide ions is 100 times higher than in a water with a pH of 11.

As mentioned earlier, K_w it depends on the temperature. If the pH of an aqueous solution is measured at 25 ° C and another measurement is made to this same water at 50 ° C, the pH value will be different. The following table shows values of pK_w values as a function of temperature.

Changes of the constant pK_w depending on the temperature

 

Examples of pH application

1. With a volumetric pipette, we add 10 ml of sulfuric acid (H₂SO₄) to 98% in a 1-liter volumetric flask. We make up with distilled and degassed water. The laboratory temperature is 20 ° C. What pH will the solution have?

Answer:

H density₂SO₄ to 98% at 20 ° C: 1.84 g / cm³.

Mass of H₂SO₄  to added 98% = 10 cm³ x 1.84 g / cm³ = 18.4 g.

When percentages in liquids or solids are reported, if no clarification is made, it is referred to as % by weight. Therefore, the mass of pure sulfuric acid added to the flask is:

 

 

 

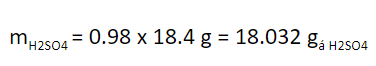
We convert to mole, dividing by the molar mass of H₂SO₄ (98 g / mol):

 

 

 

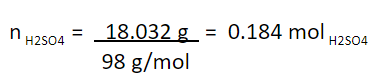
Molar concentration of the solution obtained: 0.184 mol H₂SO₄/ L.

Strong acids, such as sulfuric, completely dissociate in water. Therefore, all the hydrogen that is part of this acid will remain as an ion. From this, the hydrogen concentration in the solution will be:

 

 

 

 

 

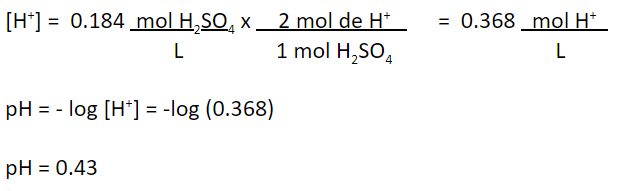
2. You have water with a pH of 13.7. It is known that it was obtained by mixing a 50% liquid soda (NaOH) solution with distilled and degassed water. The temperature is 25 ° C. What is the concentration of soda in the solution, in terms of mg NaOH / L?

Answer:

pH = 13.7

At 25 ° C,

pH + pOH = 14.0

pOH = 14 – pH = 14 – 13.7

pOH = 0.3

pOH = -log [OH^–]

 

 

 

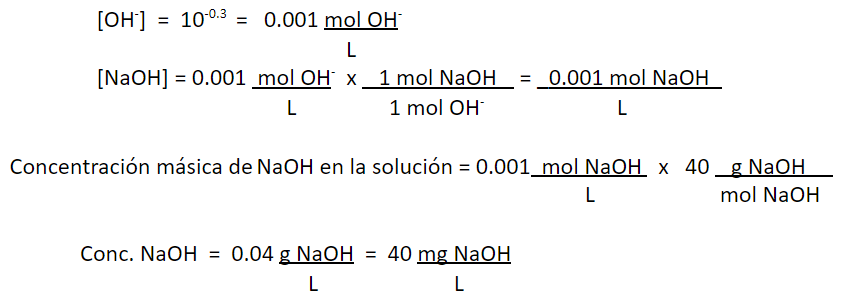
Source: https://es.wikipedia.org/wiki/PH